# 栈

# 栈的定义

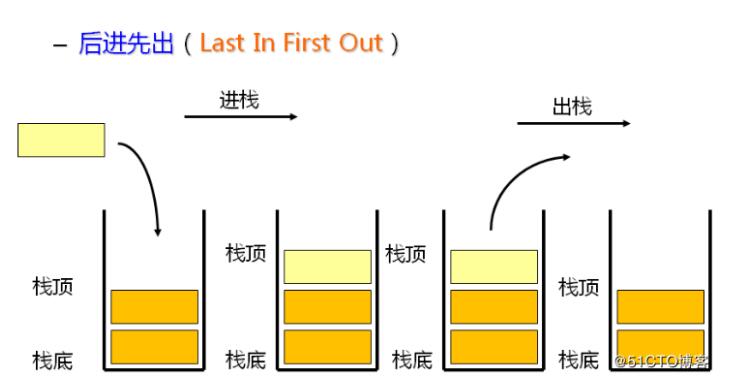
栈是一种特殊的线性表，仅能够在栈顶进行操作，有着先进后出（后进先出）的特性，下面这张图展示了栈的工作特点：

# 栈的实现

数据存储

从数据的存储的角度看，实现栈有两种方式，一种是以数组作基础，一种是以链表做基础，数组是最简单的实现方式，这里用数组来实现。

定义 Stack 类

class Stack {
  construtor() {
    this.items = []; // 使用数组存储数据
  }
}

1
2
3
4
5

# 栈的方法

栈有以下几个方法：

push(item) 添加一个元素到栈顶
pop() 弹出栈顶元素，返回值是这个元素
top() 返回栈顶元素
isEmpty() 判断栈是否为空
size() 返回栈的元素个数
clear() 清空栈

代码实现

class Stack {
  construtor() {
    this.items = []; // 使用数组存储数据
  }

  push(item) {
    this.items.push(item);
  };

  pop() {
    return this.items.pop();
  };

  top() {
    return this.items[this.items.length - 1];
  };

  isEmpty() {
    return this.items.length === 0;
  };

  size() {
    return this.items.length;
  };

  clear() {
    this.items.length = 0;
  };
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 栈的应用练习

# 合法括号

下面的字符串中包含小括号，请编写一个函数判断字符串中的括号是否合法，所谓合法，就是括号成对出现。

s(df(adc)(ff)(ddd)ff) // 合法
()()ab((sadf)safd)) // 不合法
sadf)((asdf)(asfd) // 不合法

1
2
3

思路

遇到左括号，就把左括号压如栈中。
遇到右括号，判断栈是否为空，为空说明没有左括号与之对应，缺少左括号，字符串括号不合法；如果栈不为空，则把栈顶元素移除，这对括号就抵消掉了。
当循环结束后，如果栈是空的，则所有左右括号都抵消掉了，如果栈里还有元素，则缺少右括号，字符串括号不合法。

function isLeaglBrackets(string) {
  var stack = new Stack();
  for (var i = 0; i < string.length; i++) {
    var item = string[i];
    if (item === "(") {
      // 将左括号压入栈中
      stack.push(item);
    } else if (item === ")") {
      // 如果栈为空，就说明没有左括号与之抵消
      if (stack.isEmpty()) {
        return false;
      } else {
        // 将栈顶的元素弹出
        stack.pop();
      }
    }
  }
  return stack.size() === 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 计算逆波兰表达式

逆波兰表达式，也叫后缀表达式，它讲复杂表达式转换为可以依靠简单操作得到计算结果的表达式，例如(a+b)*(c+d)转为 ab+cd+*.

示例：

["4", "15", "5", "/", "+"]; // 等价于 4 + (15 / 5) 值为7

思路

遍历数组，对每一个做如下操作：

如果元素不是 + - / * 中的某一个，就压入栈中。
如果元素是 + - / * 中的某一个，记为 item，则从栈中连续弹出两个元素，记为 value1、value2，并对这两个元素做 value2 item value1 这个表达式计算，讲计算结果压入栈中。
循环结束之后，栈中只有一个元素，这个就是整个表达式的计算结果。

function calcExp(exp) {
  var stack = new Stack();
  for (var i = 0; i < exp.length; i++) {
    var item = exp[i];

    if (["+", "-", "/", "*"].indexOf(item) >= 0) {
      // 从栈顶弹出两个元素
      var value1 = stack.pop();
      var value2 = stack.pop();
      var res = eval(value2 + item + value1);
      // 将计算结果压入栈
      stack.push(res);
    } else {
      stack.push(item);
    }
  }
  return stack.pop();
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 实现一个有 min 方法的栈

实现一个栈，除了常见的 push，pop 方法外，提供一个 min 方法，返回栈里最小的元素，且时间复杂度为 O(1)。

思路

使用两个栈来存储数据，其中一个命名为 dataStack，专门用来存储数据，另个命名为 minStack，专门用来存储栈里最小的数据。

分析过程：

我们要实现的一个栈，除了常规的方法，还要一个 min 方法，dataStack 就是专门为常规方法而存在的，minStack 就是为了这个 min 方法而存在的。
编程思想里有个分而治之的思想，简单来说，就是分开像，分开处理。那么我们现在考虑 dataStack，这个时候别管 min 方法，你就只关心 dataStack，它就是一个普遍的栈。minStack 它要存储栈里最小值，我们先考虑边界情况，如果 minStack 为空，这个时候，如果 push 进来一个数据，那这个数据一定是最小的，所以此时直接放入 minStack 即可，如果 minStack 不为空，这个时候它的栈顶不正是栈的最小元素么，如果 push 进来的元素比栈顶元素还小，放入 minStack 就好了，这样，minStack 的栈顶始终都是栈里的最小值。

function minStack() {
  var dataStack = new Stack();
  var minStack = new Stack();

  // push的时候两个栈都要操作
  this.push = function(item) {
    dataStack.push(item);

    // 如果minStack为空，直接放入，如果item小于minStack栈顶元素，放入其中
    if (minStack.isEmpty() || item < minStack.top()) {
      minStack.push(item);
    } else {
      // 如果item大于等于栈顶元素，把minStack的栈顶元素再放入一次
      // minStack的元素个数要和dataStack保持一致
      minStack.push(minStack.top());
    }
  };

  this.pop = function() {
    dataStack.pop();
    minStack.pop();
  };

  this.min = function() {
    return minStack.top();
  };
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 中缀表达式转后缀表达式

例如

输入：["12", "+", "3"]
输出：["12", "3", "+"]

输入：["(", "1", "+", "(", "4", "+", "5", "+", "3", ")", "-", "3", ")", "+", "(", "9", "+", "8", ")"]
输出：['1', '4', '5', '+', '3', '+', '+', '3', '-', '9', '8', '+', '+']

1
2
3
4
5

思路

定义数组 postfixList，用于存储后缀表达式，遍历中缀表达式，对每一个遍历到的元素做如处理：

如果是数字，直接放入 postfixList 中。
遇到左括号入栈。
遇到右括号，把栈顶元素弹出并放入到 postfixList 中，知道遇到左括号，最后弹出左括号。
遇到运算符，把栈顶的运算符弹出，知道栈顶的运算符优先级小于当前运算符，把弹出的运算符加入到 postfixList，当前的运算符入栈。
循环结束后，栈里可能还有元素，都弹出放入到 postfixList 中。

//  定义运算符的优先级
var priorityMap = {
  "+": 1,
  "-": 1,
  "*": 2,
  "/": 2
};

function infixExp2PostfixExp(exp) {
  var stack = new Stack();
  var postfixList = [];
  for (var i = 0; i < exp.length; i++) {
    var item = exp[i];
    //  如果是数字,直接放入到postfixList中
    if (!isNaN(item)) {
      postfixList.push(item);
    } else if (item === "(") {
      //  遇到左括号入栈
      stack.push(item);
    } else if (item === ")") {
      //  遇到右括号,把栈顶元素弹出,直到遇到左括号
      while (stack.top() !== "(") {
        postfixList.push(stack.pop());
      }
      stack.pop(); //  左括号出栈
    } else {
      //  遇到运算符,把栈顶的运算符弹出,直到栈顶的运算符优先级小于当前运算符
      while (
        !stack.isEmpty() &&
        ["+", "-", "*", "/"].indexOf(stack.top()) >= 0 &&
        priorityMap[stack.top()] >= priorityMap[item]
      ) {
        //  把弹出的运算符加入到postfixList
        postfixList.push(stack.pop());
      }
      //  当前的运算符⼊栈
      stack.push(item);
    }
  }
  //  for循环结束后, 栈⾥可能还有元素,都弹出放⼊到postfixList中
  while (!stack.isEmpty()) {
    postfixList.push(stack.pop());
  }
  return postfixList;
}
//  12+3
console.log(infixExp2PostfixExp(["12", "+", "3"]));
//  2-3+2
console.log(infixExp2PostfixExp(["2", "-", "3", "+", "2"]));
//  (1+(4+5+3)-3)+(9+8)
var exp1 = [
  "(",
  "1",
  "+",
  "(",
  "4",
  "+",
  "5",
  "+",
  "3",
  ")",
  "-",
  "3",
  ")",
  "+",
  "(",
  "9",
  "+",
  "8",
  ")"
];
console.log(infixExp2PostfixExp(exp1));
//  (1+(4+5+3)/4-3)+(6+8)*3
var exp2 = [
  "(",
  "1",
  "+",
  "(",
  "4",
  "+",
  "5",
  "+",
  "3",
  ")",
  "/",
  "4",
  "-",
  "3",
  ")",
  "+",
  "(",
  "6",
  "+",
  "8",
  ")",
  "*",
  "3"
];
console.log(infixExp2PostfixExp(exp2));
console.log(infixExp2PostfixExp(["12", "+", "3", "*", "5"]));
console.log(infixExp2PostfixExp(["12", "*", "3", "+", "5"]));

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

队列 →