# 二叉搜索树

# 介绍

二叉搜索树（BST）是二叉树的一种特殊表示形式，它满足如下特性：

特性

每个节点中的值必须大于（或等于）存储在其左侧子树中的任何值。
每个节点中的值必须小于（或等于）存储在其右子树中的任何值。

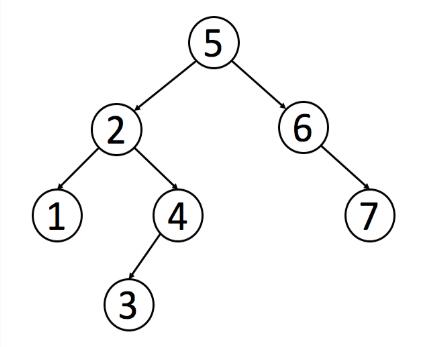
下面是一个二叉搜索树的例子：

# 实现二叉搜索树

// 节点类
class BSTNode {
  constructor(node) {
    this.val = node;
    this.left = null;
    this.right = null;
  }
  // 比较两个节点
  compare(node) {
    return this.val - node.val;
  }
}

1
2
3
4
5
6
7
8
9
10
11
12

// 二叉搜索树
class BST {
  constructor() {
    this.root = null;
    this.size = 0;
  }
  // 添加节点
  add(val) {
    const that = this;
    this.root = _add(this.root, new BSTNode(val));

    function _add(node, newNode) {
      if (node === null) {
        that.size++;
        return newNode;
      }
      if (newNode.compare(node) < 0) {
        node.left = _add(node.left, newNode);
      } else if (newNode.compare(node) > 0) {
        node.right = _add(node.right, newNode);
      }
      return node;
    }
  }
  // 是否包含节点
  contains(val) {
    return this.depth(val) > -1;
  }
  // 查找深度，不存在返回-1
  depth(val) {
    return _findDepth(this.root, new BSTNode(val), 0);

    function _findDepth(node, newNode, depth) {
      if (node === null) {
        return -1;
      }
      if (newNode.compare(node) === 0) {
        return depth;
      } else if (newNode.compare(node) < 0) {
        return _findDepth(node.left, newNode, depth + 1);
      } else {
        return _findDepth(node.right, newNode, depth + 1);
      }
    }
  }
  // 前序遍历
  preOrder(cb) {
    _preOrder(this.root, cb);

    function _preOrder(node, cb) {
      if (node === null) {
        return;
      }
      typeof cb === "function" && cb(node);
      _preOrder(node.left, cb);
      _preOrder(node.right, cb);
    }
  }
  // 非递归前序遍历(深度优先)
  preOrderNR(cb) {
    const stack = [];
    if (this.root === null) {
      return;
    }
    stack.push(this.root);
    while (stack.length) {
      var node = stack.pop();
      typeof cb === "function" && cb(node);
      if (node.right !== null) {
        stack.push(node.right);
      }
      if (node.left !== null) {
        stack.push(node.left);
      }
    }
  }
  // 层序遍历(广度优先)
  leveOrder(cb) {
    const queue = [];
    if (this.root === null) {
      return;
    }
    queue.push(this.root);
    while (queue.length) {
      var node = queue.shift();
      typeof cb === "function" && cb(node);
      if (node.left !== null) {
        queue.push(node.left);
      }
      if (node.right !== null) {
        queue.push(node.right);
      }
    }
  }
  // 中序遍历，结果从小到大
  inOrder(cb) {
    _inOrder(this.root, cb);

    function _inOrder(node, cb) {
      if (node === null) {
        return;
      }
      _inOrder(node.left, cb);
      typeof cb === "function" && cb(node);
      _inOrder(node.right, cb);
    }
  }
  // 后序遍历
  postOrder(cb) {
    _postOrder(this.root, cb);

    function _postOrder(node, cb) {
      if (node === null) {
        return;
      }
      _postOrder(node.left, cb);
      _postOrder(node.right, cb);
      typeof cb === "function" && cb(node);
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121

# 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

# 思路

验证二叉搜索树有很多种解法，可以利用它本身的性质来做，即左<根<右，也可以通过利用中序遍历结果为有序数列来做。

# 利用其本身性质来做

初始化时带入系统最大值和最小值，在递归过程中换成它们自己的节点值，

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function(root) {
  return _isValidBST(root, -Number.MAX_VALUE, Number.MAX_VALUE);

  function _isValidBST(root, min, max) {
    if (root === null) return true;
    if (root.val <= min || root.val >= max) return false;
    return (
      _isValidBST(root.left, min, root.val) &&
      _isValidBST(root.right, root.val, max)
    );
  }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 利用中序遍历结果为有序数列

递归实现

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function(root) {
  var res = true;
  var preNode = null;
  inorder(root);
  return res;

  function inorder(root) {
    if (root === null) return;
    inorder(root.left);
    if (preNode === null) {
      preNode = root;
    } else {
      if (root.val <= preNode.val) {
        res = false;
        return;
      }
      preNode = root;
    }
    inorder(root.right);
  }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

非递归实现，需要用到栈

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function(root) {
  var stack = [];
  var preNode = null;
  var p = root;

  while (stack.length || p !== null) {
    while (p !== null) {
      stack.push(p);
      p = p.left;
    }
    var top = stack.pop();

    if (preNode && top.val <= preNode.val) {
      return false;
    }
    preNode = top;
    p = top.right;
  }
  return true;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 二叉搜索树迭代器

二叉搜索树迭代器。将使用二叉搜索树的根节点初始化迭代器。调用 next() 将返回二叉搜索树中的下一个最小的数。

1
2
3
4
5

BSTIterator iterator = new BSTIterator(root);
iterator.next();    // 返回 3
iterator.next();    // 返回 7
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 9
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 15
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 20
iterator.hasNext(); // 返回 false

1
2
3
4
5
6
7
8
9
10

提示

next() 和 hasNext() 操作的时间复杂度是 O(1)，并使用 O(h) 内存，其中 h 是树的高度。
可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 中至少存在一个下一个最小的数。

# 实现一个二叉搜索树迭代器

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 */
class BSTIterator {
  construtor(root) {
    this.s = [];
    while (root) {
      this.s.push(root);
      root = root.left;
    }
  }

  next() {
    if (!this.hasNext()) {
      return null;
    }
    var top = this.s.pop();
    var res = top;
    if (top && top.right) {
      top = top.right;
      while (top !== null) {
        this.s.push(top);
        top = top.left;
      }
    }
    return res.val;
  }

  hasNext() {
    return this.s.length > 0;
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

← 二叉树